Задачи о раскрасках
Каждую грань кубика разбили на четыре равных квадрата и раскрасили эти квадраты в три цвета так, чтобы квадраты, имеющие общую сторону, были покрашены в разные цвета. Докажите, что в каждый цвет покрашено по 8 квадратиков. Можно ли покрасить четыре вершины куба в красный цвет и четыре другие — в синий так, чтобы плоскость, проходящая через любые три точки одного цвета, содержала точку другого цвета? Авторы: Мёбиус А. Автор: Митягин А.










Используйте шахматную раскраску. Воспользуйтесь раскраской 1. Воспользуйтесь раскраской 3. Воспользуйтесь раскраской 4. Воспользуйтесь раскраской 2. Воспользуйтесь раскраской 5.
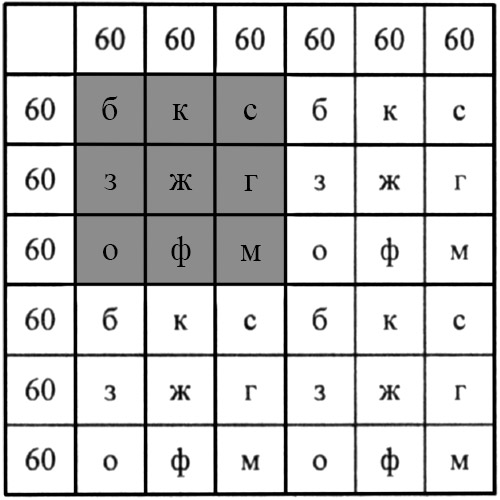








Петя хочет передвинуть каждую фишку на соседнюю по стороне клетку так, чтобы снова в каждой из клеток оказалось по одной фишке. Сможет ли Петя это сделать? Докажите что для любых m и n можно так раскрасить бесконечную клетчатую доску в 2 цвета для каждых конкретных m и n своя раскраска , что всегда 2 клетки, соединенные одним ходом крокодила, будут покрашены в разные цвета. Автор: Ботин Д. Белого "Разноцветная математика" Подтемы: Шахматная раскраска 93 задачи Вспомогательная раскраска прочее 62 задачи Фильтр Сложность с 1 2 3 4 5 6 7 8 9 10 по 1 2 3 4 5 6 7 8 9 10 Класс с 5 6 7 8 9 10 11 по 5 6 7 8 9 10 Шахматная раскраска.