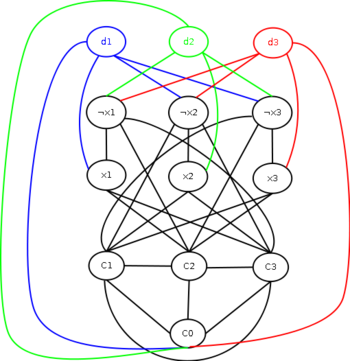
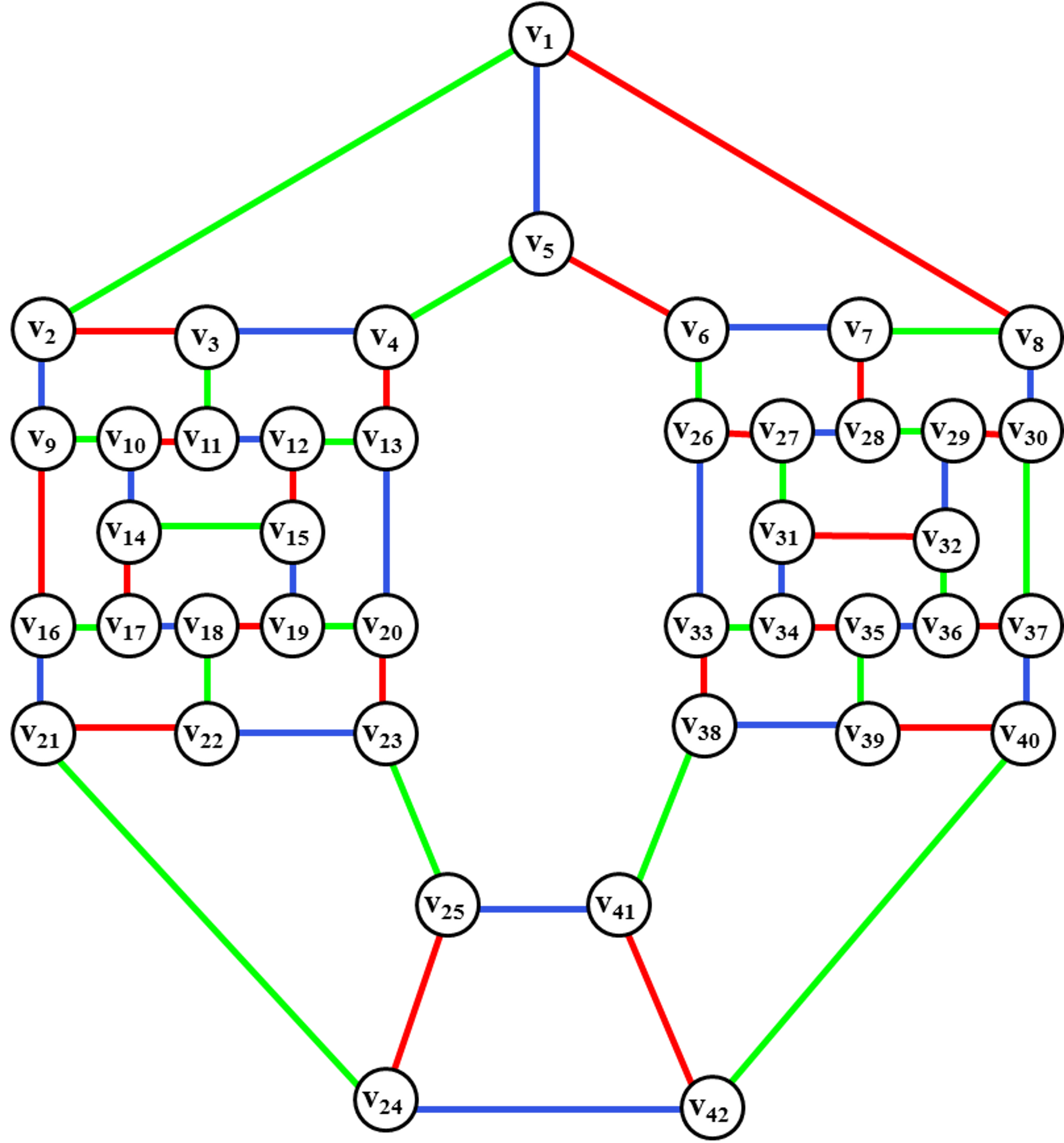
Раскраска вершин графа
При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин. Довольно часто дополнительно требуется, чтобы таких классов было наименьшее число. В теории графов подобные задачи формулируются в терминах раскраски вершин графа. Число k — число красок раскраски f.
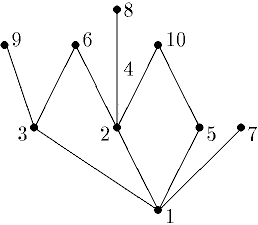
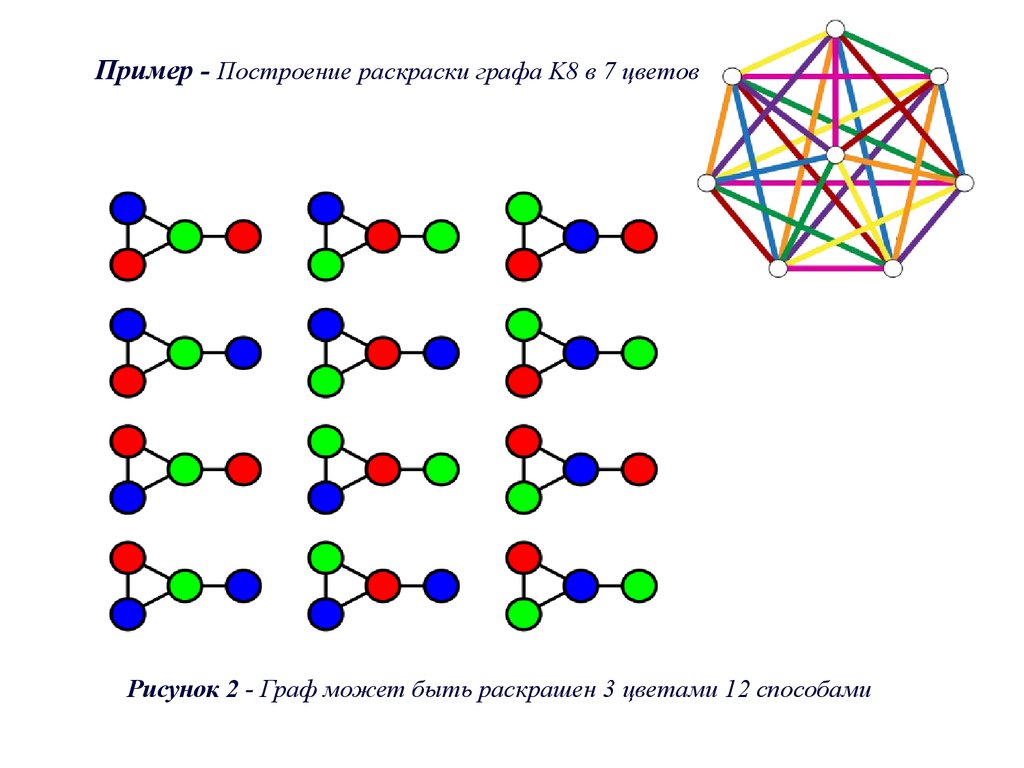
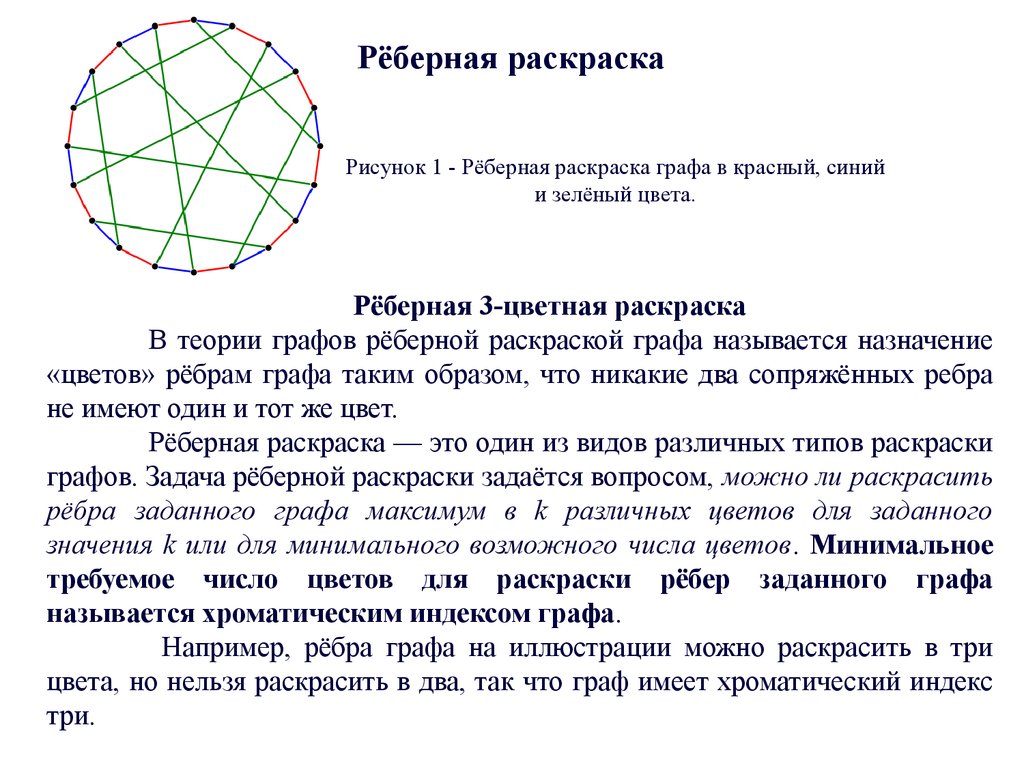
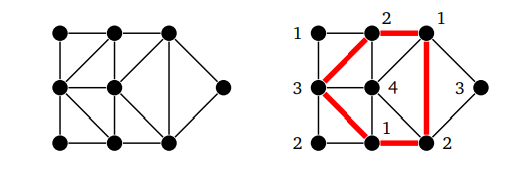
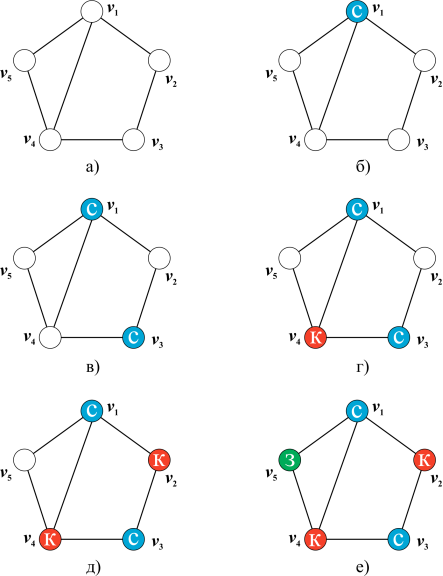
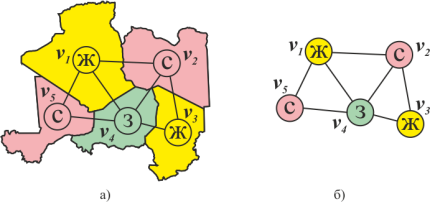
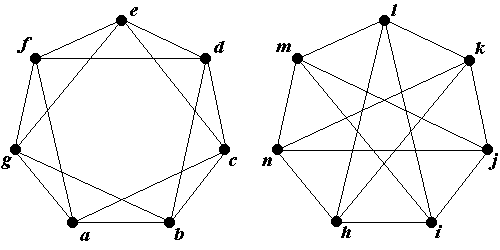
Правильная вершинная рёберная раскраска — это раскраска вершин рёбер графа, при которой любые смежные вершины рёбра окрашены в разные цвета. Правильную вершинную раскраску часто называют просто раскраской графа. Граф называется k k k -раскрашиваемым, если существует правильная вершинная раскраска графа k k k цветами. Граф является 2 2 2 -хроматическим тогда и только тогда, когда он не содержит простых циклов нечётной длины. Пусть f G , t f G, t f G , t — число различных правильных раскрасок графа G G G с нумерованными вершинами в t t t или меньше цветов, тогда для любого графа G G G функция f G , t f G, t f G , t есть многочлен от переменной t t t , называемый хроматичеcким многочленом графа G G G.
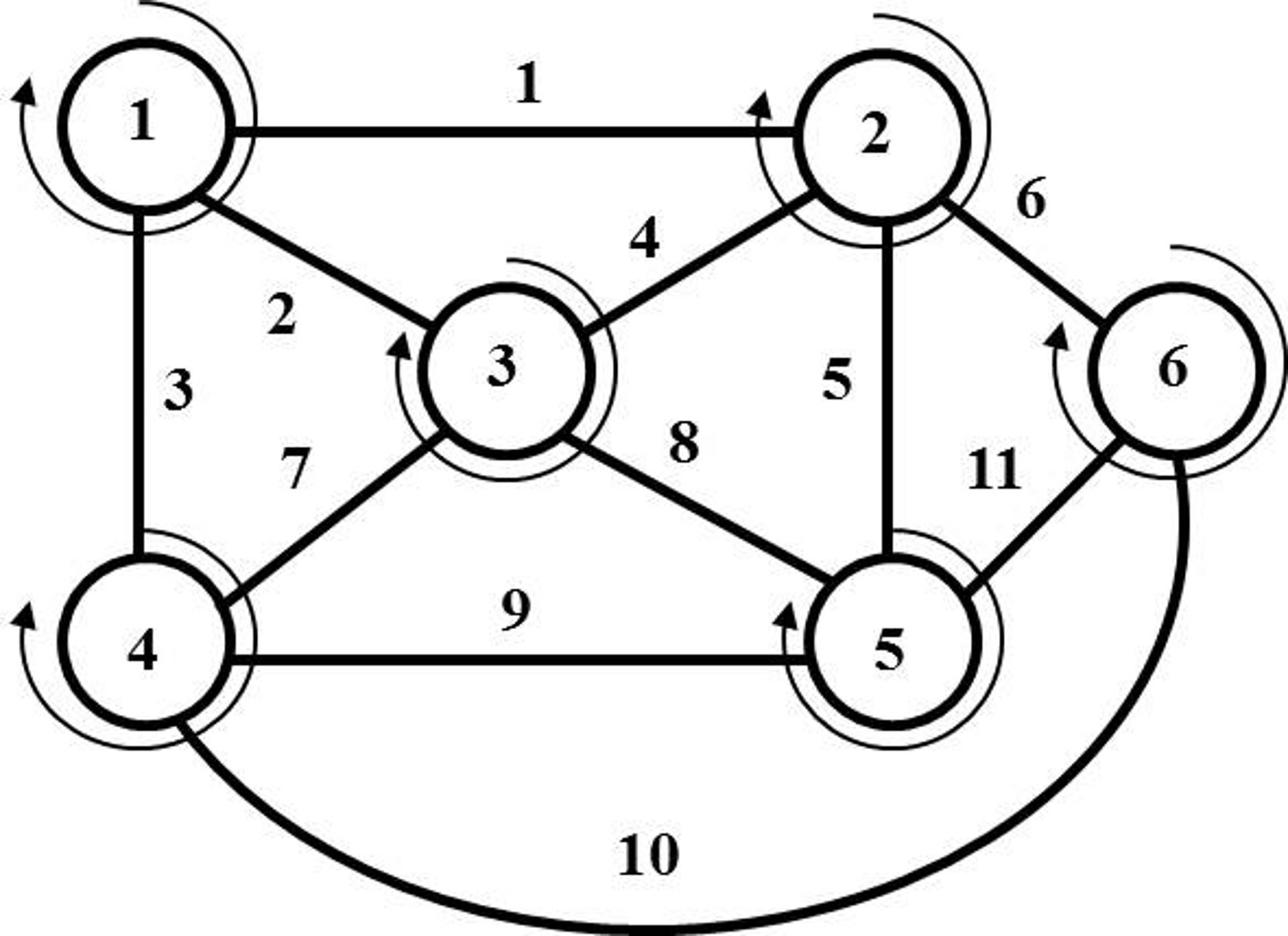

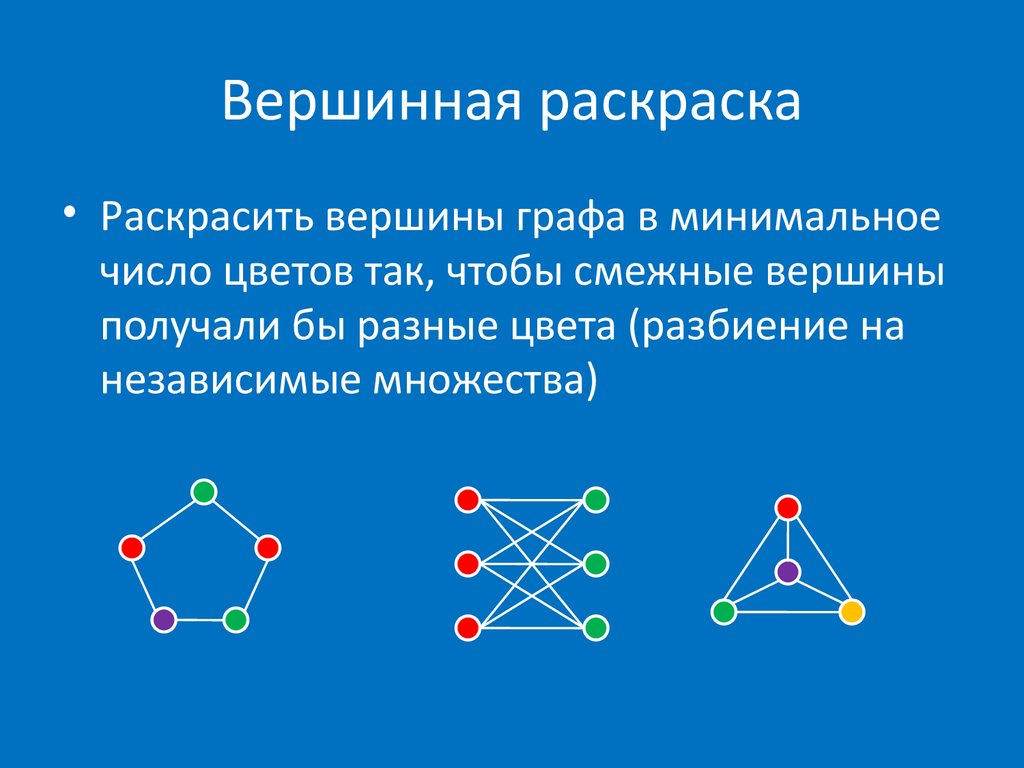



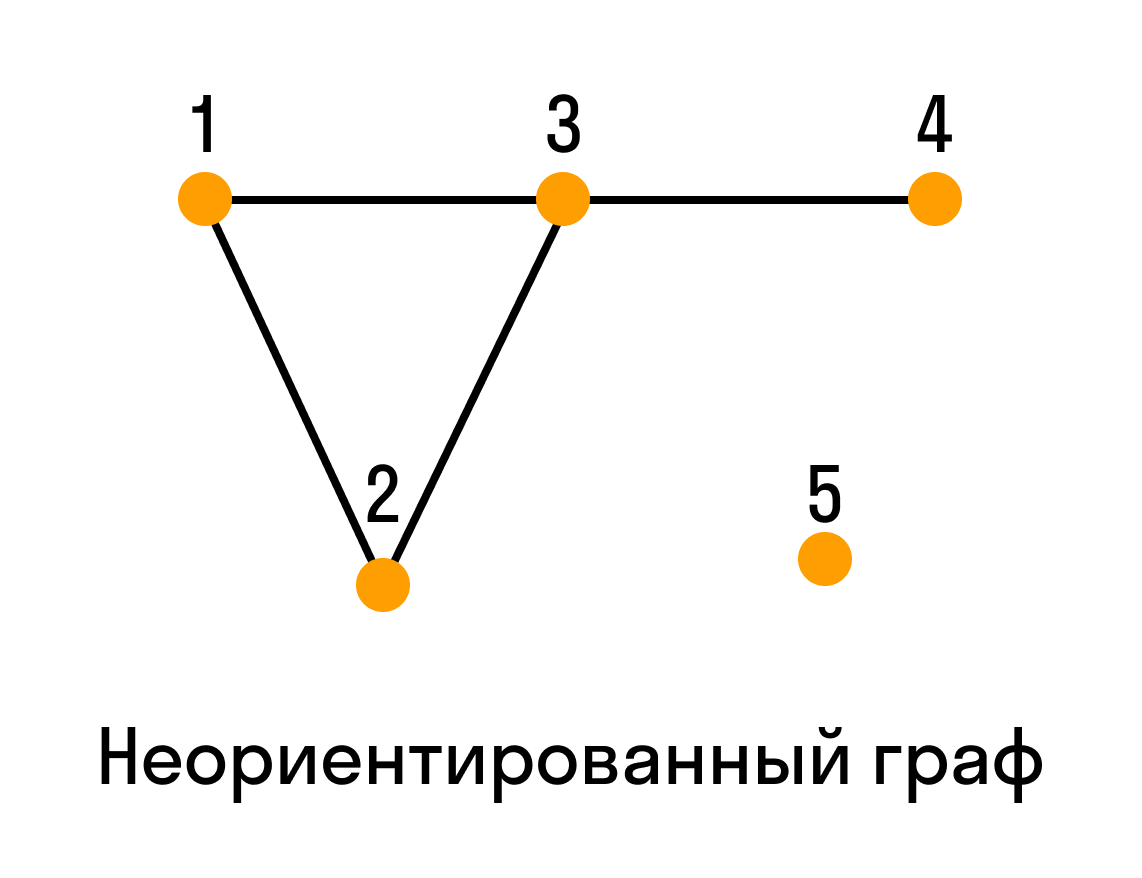
В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается. Цвета — это целые положительные цифры. Графы нужно раскрашивать так, чтобы соседние вершины имели разные цвета. Еще стоит использовать как можно меньше цветов. Первый пример на схеме выше не совсем верный, потому что соседним вершинам присваивается один и тот же цвет.